ENERO

FECHA: 03/01/2017

MÁXIMOS Y MÍNIMOS ABSOLUTOS 

Toda función diferenciable en una región acotada y cerrada alcanza su valor máximo (o mínimo), o en un punto estacionario o en un punto de la frontera de la región.

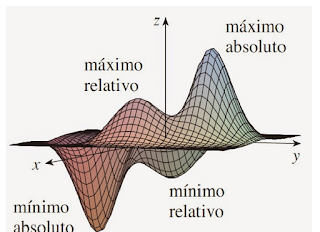
Si f(x,y) es una función continua en un conjunto D cerrado y acotado en R2, entonces f alcanza un valor máximo absoluto f(x,y) y un valor mínimo absoluto f(x,y) en algunos puntos (x1,y1) y (x2,y2) en D.

Para determinar estos valores máximos y mínimos absolutos:

1.- Se calcula los valores de f en los puntos críticos de f en D.

2.- Se determinan los valores extremos de f en la frontera de D.

3.- El más grande de lo valores de los puntos 1 y 2 es el Mabs (máximo absoluto) y el menor de los valores es el mabs (mínimo absoluto).

Ejemplo:

Determinar los valores máximos y mínimos absolutos de:

Calculamos los puntos críticos

Calculamos las derivadas parciales de f:

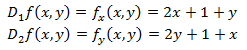
Los puntos críticos son aquellos que anulan a las derivadas parciales. Por tanto, igualamos a 0 las derivadas parciales para obtener un sistema de ecuaciones:

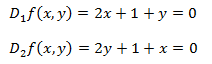
Resolvemos el sistema y obtenemos el punto crítico

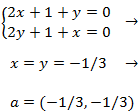
Calculamos el Hessiano y aplicamos el teorema

Evaluamos las derivadas parciales segundas en dicho punto:

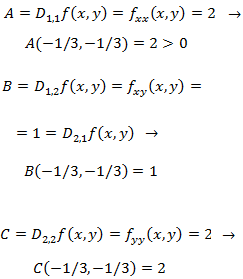
Por tanto, el Hessiano en dicho punto es

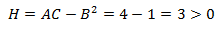
Con lo que, aplicando el teorema, el punto es un mínimo relativo.

PRESENTACIÓN

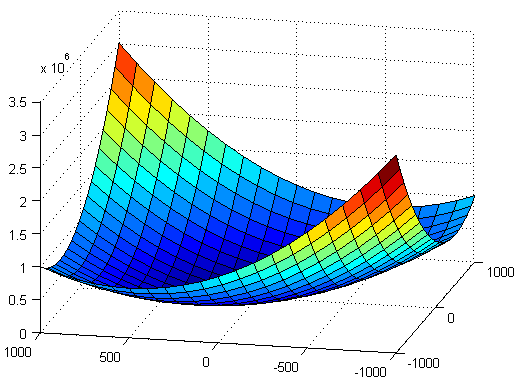
c

MÁXIMOS Y MÍNIMOS CONDICIONALES 

Método de multiplicadores de Lagrange.

Para determinar los valores máximos y mínimos de f(x,y) sujeto la restricción (condición) g(x,y)=0 (Ec de enlace), suponiendo que estos valores existen y que el gradiente de (g) sea diferente de cero, se debe resolver el siguiente sistema de ecuaciones.

- El valor mayor de f(x,y) en estos puntos es el máximo condicionado y el menor valor de f(x,y) es el mínimo condicionado.

- λ: Multiplicador de langrage, valor constante diferente de cero.

- Al plantear la ecuación 1, se está afirmando que el gradiente de f y g son vectores paralelos entre sí.

- El vector gradiente de f es ortogonal al vector tangente r`(to) a toda curva.

- La ecuación de enlace g(x,y)=0, representa la condición o restricción del problema y esta relaciona las variables independientes (x) y (y).

- El número de restricciones debe ser menor al número de variables.

Ejemplo: 

FECHA: 06/01/2017

INTEGRALES MÚLTIPLES

En R^2

f: A→B

    x→y=f(x)

Al igual que las integrales de una variable sirven para calcular el área bajo una gráfica, las integrales dobles sirven para calcular volúmenes.

Concretamente, cuando F ≥ 0, la integral ∫ d c ∫ b a F(x, y) dxdy es el volumen bajo la gráfica en el rectángulo [a, b] × [c, d], esto es, a ≤ x ≤ b, c ≤ y ≤ d. Lo mismo se cumple en regiones más generales. Es decir, si R es una región del plano y F = F(x, y) es una función no negativa en ella, entonces (1) ∫∫ R F = Volumen bajo la gráfica de F sobre la región R.

En R^3

f=D ⊆ R^2 → R

    (x,y)→ z=f(x,y)

FECHA:10/01/2017

INTEGRAL TRIPLE

Las integrales múltiples se utilizan en muchas aplicaciones, en áreas de ciencias de ingeniería:

🔼Cálculo de áreas.

🔼Cálculo de volúmenes.

🔼Cálculo de masas, centros de masa.

🔼Cálculo de promedios

🔻Si f(x,y) es positiva en la región R, entonces la integral ∫∫f(x,y)dA da una aproximación de R volumen del sólido acotado por las superficie z=f(x,y) y el plano OXY.

🔻Si f(x,y) es continua en la región cerrada R, entonces es integrable en R,

Tipos de regiones de integración

Regiones rectangulares

R={(x,y)∈ R^2/ a≤ x ≤ b, c ≤y ≤b}

Integrales Iteradas.

REGIONES MÁS GENERALES

FECHA:13/01/2017

Coordenadas rectangulares  a Coordenadas polares

Coordenadas Cilíndricas:

Coordenadas Esféricas 

FECHA: 17/01/2017

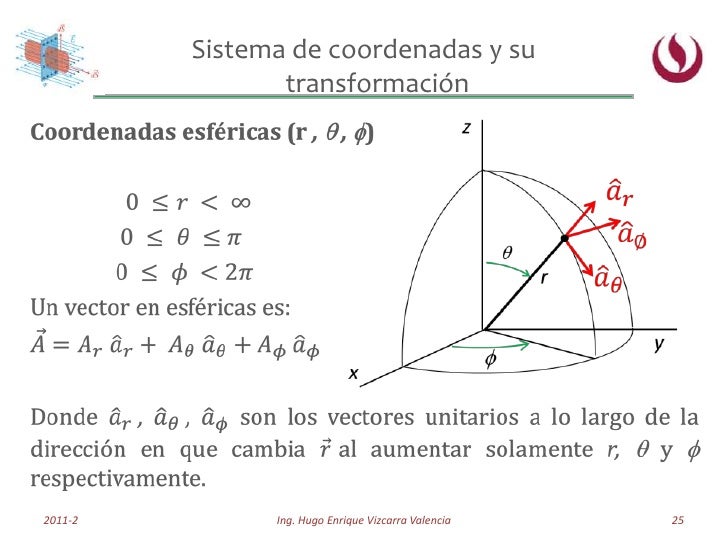
Coordenadas rectangulares  a Coordenadas esféricas

FECHA:20/01/2017

APLICACIONES

1) Cálculo de áreas planas

2) Cálculo de áreas volúmenes

3) Cálculo de áreas centro de masa

4) Cálculo de momentos de inercia

5) Cálculo de probabilidades

Centros de masa

Caso  discreto 

Para un sistema discreto la posición del centro de masas (CM) viene dada por la expresión

donde m_i es la masa de cada partícula y  su vector de posición. Cuando tratamos con un sistema continua, la expresión se transforma según el cambio

Caso continuo 

en un sistema continuo la posición del centro de masas viene dada por la expresión

siendo  un vector que recorre cada uno de los puntos del sistema y dm la masa infinitesimal asociada a cada uno de esos puntos.

Ejercicio :

FECHA:24/01/2017

DISTRIBUCIÓN DE MASA LINEAL

 LINEAL 

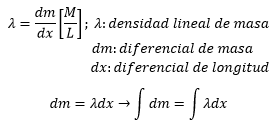
 SUPERFICIAL 

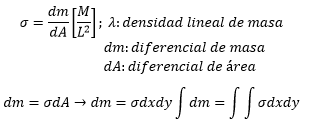
 VOLUMETRICA 

FECHA: 27/01/2017

MOMENTOS DE INERCIA

1._ Masas puntuales

Los momentos de inercia de las “n” masas respecto a los ejes coordenados:

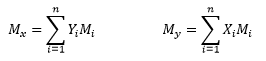
2._ Masa continúa

Sea L una lámina los momentos de inercia con respecto a los ejes coordenados son:

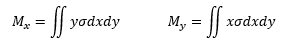
FECHA:31/01/2017

CAMPOS VECTORIALES

Sirven  para representar fenómenos naturales como :

Rapidez y dirección del viento.

Magnitud del cuerpo gravitacional en diferentes lugares sobre la superficie terrestre.

Flujo del viento alrededor de alerones de aviones.

Flujo de corrientes marinas.

En general en CAMPO VECTORIAL es una función cuyo dominio es un conjunto de puntos en R^2 o R^3 y cuyo rango es un conjunto de vectores en V2 0 V3.

Campos Vectoriales conservativos

DIVERGENCIA Y ROTACIONAL DE CUERPOS VECTORIALES

Divergencia

 Ejemplo:

 

Rotacional de un campo vectorial conservativo

Ejercicios:

 

Laplaciano de un campo vectorial conservativo