FECHA:1 DE NOVIEMBRE DEL 2016
RECTA DETERMINADA POR DOS PLANOS
A partir de dos planos vamos demostramos la ecuación de la recta (L) de intersección de el plano 1 y 2.
Para lo cual primero procedemos a sacar el vector director de la recta, realizando el producto cruz de los vectores normales del plano 1 y 2.
a= n1xn2 = (l ,m, n)
Tomamos un punto sobre la recta (L)
Si y=0 entonces A1X+C1Z+D1=0 y A2X+C2X+D2=0
El punto P1(x1, o, z1) va tener el vector dirección posición r1=(x1, o, z1)
Entonces:
r=r1+t(a)
r= (x1, o, z1) + t (a)
Tenemos las ecuaciones paramétricas de la recta (L)
x= x1 + t (l)
y= o + t (m)
z= z1 + t (n)
Despejando la (t) obtendremos las ecuaciones simétricas de la recta (L)
(x-x1)/l = (y-0)/m = (z-z1)/n
HAZ DE PLANOS
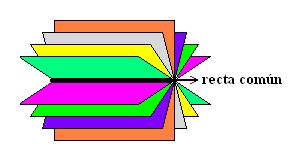
Para determinar su ecuación se necesita las ecuaciones de dos planos 1 y 2
Multiplicamos al primer plano por alfa y al segundo plano por beta y sumamos las ecuaciones
Realizamos un cambio de variable
Y obtenemos la ecuación del haz del plano
Y también su vector normal
ECUACIÓN VECTORIAL DE LA ESFERA
Partiendo de un centro =(X0, Y0, Z0) con un radio=r
Obtenemos la ecuación vectorial de la esfera que es igual a
(r1-r0)^2 =r^2
ro=vector posición del centro de la esfera.
r1=vector posición de un punto alrededor de la esfera.
Además podemos encontrar la Ecuación general de la esfera
FECHA: 8 DE NOVIEMBRE DEL 2016
SUPERFICIES DE SEGUNDO ORDEN
Se llaman así a las superficies el espacio que vienen dadas por ecuaciones de segundo grado:
Ax^2+ By^2+Cz^2+2Dxy+2Exz+2Fyz+2Gx+2Hy+2Kz+1=0
Para realizar el análisis de estas superficies se debe seguir el siguiente procedimiento:
1.-Intersección con los ejes coordenados.
2.-Intersección con los planos coordenados ( YOZ, XOZ, XOY)
3.-Intersección con planos paralelos a los planos coordenados.
4.-Bosquejo
Se llaman así a las superficies en el espacio que vienen dadas por ecuaciones de segundo grado
Para realizar el análisis de estas superficies se debe seguir el siguiente procedimiento con un ejemplo.
1.-Intersección con los ejes coordenados
i) Intersección con el eje OX
ii) Intersección con el eje OY
iii) Intersección con el eje XY


2.-Intersección con los planos coordenados
i) Intersección con el plano XOY
ii) Intersección con el plano XOZ
iii) Intersección con el plano YOZ


3.-Intersección con los planos paralelos a los planos coordenados
i) Intersección con los planos paralelos a los planos XOY
Donde Z=K
ii) Intersección con los planos paralelos a los planos XOZ
Donde Y=K
iii) Intersección con los planos paralelos a los planos YOZ
Donde X=K

4.-Bosquejo de la gráfica de la superficie
Superficies más comunes:
FECHA: 15 DE NOVIEMBRE DEL 2016
FUNCIONES VECTORIALES
Se llaman función vectorial de la variable real (t), a toda función F (T) de (I) en R^n
F= I⊂R ⟶ Rn
OPERACIONES CON FUNCIONES VECTORIALES
Dadas las funciones vectoriales:
F: I ⟶ Rn ; G ; I ⟶ Rn
G: J ⟶I donde I, J pertenece R
Se define
1.- (F+G)(t)=[f1(t)+g1(t), f2(t)+g2(t)+…..fn(t)+gn(t)]
2.- (cF(t)=[cf1(t), cf2(t)+…..cfn(t)] donde ( c ) pertenece a todos los reales
3.- (F/G)(t)=
4.- [F(t)]=[f1(t)^2+f2(t) ^2+f3(t) ^2+…..fn(t) ^2]^1/2
Si n=3
5.- (FxG) (t) = F (t) x G(t)
6.- (Fog)(t)=F(g(t))= (f1(g(t))+f2(g(t))+f3(g(t))+…..fn(g(t)))
.
FECHA: 18 DE NOVIEMBRE DEL 2016
LÍMITE DE UNA FUNCIÓN VECTORIAL

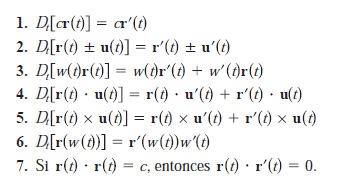
CONTINUIDAD DE UNA FUNCIÓN VECTORIAL
DERIVADA DE UNA FUNCIÓN VECTORIAL

Observaciones
1.-Una función vectorial es derivable si cada una de sus componentes existe su límite.
2.-La derivada se define como:
3.-Las propiedades y reglas de derivación de las funciones vectoriales son las mismas que las funciones reales de una variable.
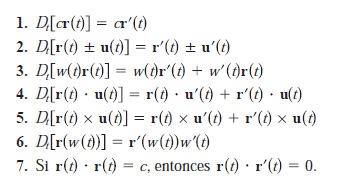
Podemos concluir con que la derivada de una función vectorial su resultado será un vector al cual podemos llamarlo vector tangente a la curva que esta definida por la función r(t) en un punto P.
INTEGRAL DE UNA FUNCIÓN VECTORIAL
La integral de una función vectorial es una familia de funciones vectoriales que difieren entre sí en un vector constante C.
FECHA: 22 DE NOVIEMBRE DEL 2016
VECTORES TANGENTE UNITARIO Y NORMAL PRINCIPAL
El vector tangente unitario se describe por T(t) y es un vector tangente ala curva.
El modulo de T(t) es igual a 1 , entonces T(t) y T`(t) son ortogonales entre si por tanto, se define el vector normal principal.
PLANO OSCULADOR
Si n=3
El plano osculador, pasa por el punto F(t) y esta generado por T(t) y N(t).
Es el plano que mayor se ajusta a la curva en una vecindad de F(t).
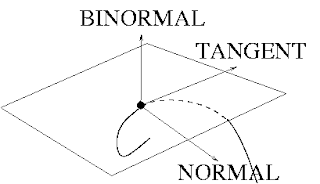
El vector binormal, es el vector definido por: B(t)= T(t)XN(t)
Cada par de vectores forman un plano:
PLANO OSCULADOR: T ^ N
PLANO NORMAL: N ^ B
PLANO RECTIFICANTE: T ^ B
Dado un vector n=(Bx,By,Bz) un punto P=(Xo,Yo,Zo)
Aplicando la formula de la ecuación de un plano (r-r1).n=0
i) ECUACIÓN. PLANO OSCULADOR: Bx(X - Xo) + By(Y - Yo) + Bz(Z - Zo) = 0
ii) ECUACIÓN. PLANO NORMAL: Tx(X - Xo) + Ty(Y - Yo) + Tz(Z - Zo) = 0
iii) ECUACIÓN. PLANO RECTIFICADOR: Nx(X - Xo) + Ny(Y - Yo) + Nz(Z - Zo) = 0
Dado un vector a=T(t)=(Tx,Ty,Tz) un punto P=(Xo,Yo,Zo)
Aplicando la formula de la ecuación de una recta r=r1+ta
iv) ECUACIÓN. RECTA TANGENTE: X=Xo+tTx ; Y =Yo+tTy ; Z=Zo+tTz
v) ECUACIÓN. RECTA NORMAL PRINCIPAL: X=Xo+tNx ; Y =Yo+tNy ; Z=Zo+tNz
vi) ECUACIÓN. RECTA BINORMAL: X=Xo+tBx ; Y =Yo+tBy ; Z=Zo+tBz
VECTOR CURVA
Variación del vector tangente unitario respecto a la longitud de arco.
La curvatura representa la variación del vector tangente respecto a la longitud de arco
El modulo del vector curvatura representa el radio de curvatura
Formula rápida para encontrar la ecuación de curvatura:
FUNCIONES REALES DE ARGUMENTOS VECTORIALES
Sea D un subconjunto de R^n, se dice que f es una función real de conjunto vectorial, si cada elemento x=(xi+x2+x3+x4…+xn) de D le corresponde un único valor real de Z.
Dominio de una Función (Df)
El Dominio de una función de varias variables es el conjunto D de todos los valores que pueden tomar las variables independientes para que la función exista.
Df={(x1,x2,…xn) € R^n/ Z= f(x1,x2,…xn)}
Rango de una Función (Rf)
Rf={z € R / Z= f(x1,x2,…xn)}
Si n=2
Df={(x,y)€ R2/x = f(x,y)}
Rf={z € R / z= f(x,y)}
Donde:
Z= valor dependiente
x,y = valor independiente
Análisis del Dominio.
i) Análisis Matemático
Es una descripción matemática del dominio de existencia de la función tomando en cuenta los intervalos donde se cumple la misma y especificando los valores que no podrá tomar las variables independientes.
ii) Análisis Gráfico
Es una descripción visual en el R2 y en R3 del dominio de existencia de la función en base al análisis matemático.
iii) Análisis Descriptivo
Es una descripción de los valores que puede tomar la función para que se cumpla la relación establecida por la función.
Curvas de nivel
Sea z=f(x,y) una función real de argumento vectorial, se define como curvas de nivel.
El conjunto de todos los puntos del plano donde f(x,y) tiene un valor constante, es decir f(x,y)=c, y se llama curva d nivel de f.
Curvas de Contorno
Son las curvas de nivel representadas en el espacio o R3.
Superficies de Nivel
Una superficie de nivel representa una ecuación f(x,y,z)=x^2+y^2+z^2 donde
w= x^2+y^2+z^2
w= valores dependientes
x,y,z =valores independientes
f: R3⟶R
(x,y,z)⟶ w= f(x,y,z)
No se puede representar gráficamente 4 dimensiones.
FECHA:29 DE NOVIEMBRE DEL 2016
LÍMITES
i) Para calcular el límite de una función f(x,y) se debe reducir al limite de una variable.
ii) Para funciones y=f(x) el entorno de acercamiento es un intervalo:
[xo-d ; xo+d]
iii) Para funciones z=f(x,y), el entorno de acercamiento es un disco
[(x,y)-(xo,yo)]
- Existen infinitos caminos o trayectorias de acercamiento a (xo,yo).
- Si por 2 caminos diferentes el valor del límite tiene valores diferentes entonces se concluye que el límite no existe.
- Si por 2 o más caminos diferentes el valor del límite tiene igual valor se debe demostrar con la definición u otro método.
CONTINUIDAD
Sea f: R2⟶R
(x,y) ⟶ z=f(x,y)
Una función de 2 variables, sea (xo,yo) €R2, entonces se dice que f(x,y) es continua si se cumple:
i) ∃ f(xo,yo)
ii) ∃ Lim f(x,y)
(x,y)⟶ (xo,yo)
iii) Lim f(x,y) = f(xo,yo)
(x,y)⟶(xo,yo)
iii) Lim f(x,y) = f(xo,yo)
(x,y)⟶(xo,yo)
Si no se cumple alguna de las condiciones entonces:
Discontinua Inevitable:
Si ∄ Lim f(x,y)
(x,y)⟶(xo,yo)
Discontinua Evitable:
i) ∃ Lim f(xo,yo) ∧ ∃ Lim f(x,y)
(x,y) ⟶(xo,yo)
Pero: Lim ≠ f(xo,yo)
(x,y) ⟶(xo,yo)
ii) ∄ f(xo,yo) ∧ ∃ Lim f(x,y)
(x,y) ⟶(xo,yo)
En los dos casos de discontinuidad evitable la función se debe re definir.















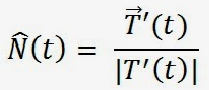






No hay comentarios:
Publicar un comentario